4.7.2.2. Mean Squared Displacement — MDAnalysis.analysis.msd

Authors:

Hugo MacDermott-Opeskin

Year:

2020

Copyright:

GNU Public License v2

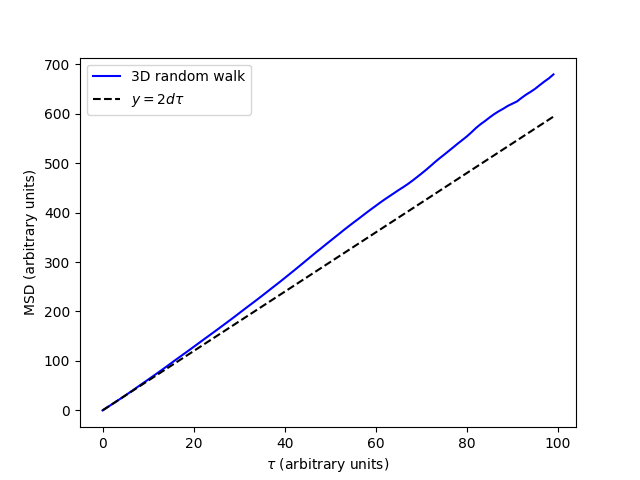
This module implements the calculation of Mean Squared Displacements (MSDs) by the Einstein relation. MSDs can be used to characterize the speed at which particles move and has its roots in the study of Brownian motion. For a full explanation of the theory behind MSDs and the subsequent calculation of self-diffusivities the reader is directed to [Maginn2018]. MSDs can be computed from the following expression, known as the Einstein formula:

\[MSD(r_{d}) = \bigg{\langle} \frac{1}{N} \sum_{i=1}^{N} |r_{d} - r_{d}(t_0)|^2 \bigg{\rangle}_{t_{0}}\]

where \(N\) is the number of equivalent particles the MSD is calculated over, \(r\) are their coordinates and \(d\) the desired dimensionality of the MSD. Note that while the definition of the MSD is universal, there are many practical considerations to computing the MSD that vary between implementations. In this module, we compute a “windowed” MSD, where the MSD is averaged over all possible lag-times \(\tau \le \tau_{max}\), where \(\tau_{max}\) is the length of the trajectory, thereby maximizing the number of samples.

The computation of the MSD in this way can be computationally intensive due to its \(N^2\) scaling with respect to \(\tau_{max}\). An algorithm to compute the MSD with \(N log(N)\) scaling based on a Fast Fourier Transform is known and can be accessed by setting fft=True [ᵇCalandrini2011, ᵇBuyl2018]. The FFT-based approach requires that the tidynamics package is installed; otherwise the code will raise an ImportError.

Please cite [ᵇCalandrini2011, ᵇBuyl2018] if you use this module in addition to the normal MDAnalysis citations.

[ᵇCalandrini2011] (1,2)

Vania Calandrini, Eric Pellegrini, Konrad Hinsen, and Gerald Kneller. nMoldyn - Interfacing spectroscopic experiments, molecular dynamics simulations and models for time correlation functions, pages 201–232. Volume 12. 01 2011. doi:10.1051/sfn/201112010.

[ᵇBuyl2018] (1,2)

Pierre Buyl. Tidynamics: a tiny package to compute the dynamics of stochastic and molecular simulations. Journal of Open Source Software, 3:877, 08 2018. doi:10.21105/joss.00877.

Warning

To correctly compute the MSD using this analysis module, you must supply coordinates in the unwrapped convention. That is, when atoms pass the periodic boundary, they must not be wrapped back into the primary simulation cell. MDAnalysis does not currently offer this functionality in the MDAnalysis.transformations API despite having functions with similar names. We plan to implement the appropriate transformations in the future. In the meantime, various simulation packages provide utilities to convert coordinates to the unwrapped convention. In GROMACS for example, this can be done using gmx trjconv with the -pbc nojump flag.

4.7.2.2.1. Computing an MSD

This example computes a 3D MSD for the movement of 100 particles undergoing a random walk. Files provided as part of the MDAnalysis test suite are used (in the variables RANDOM_WALK and RANDOM_WALK_TOPO)

First load all modules and test data

import MDAnalysis as mda
import MDAnalysis.analysis.msd as msd
from MDAnalysis.tests.datafiles import RANDOM_WALK_TOPO, RANDOM_WALK

Given a universe containing trajectory data we can extract the MSD analysis by using the class EinsteinMSD

u = mda.Universe(RANDOM_WALK_TOPO, RANDOM_WALK)
MSD = msd.EinsteinMSD(u, select='all', msd_type='xyz', fft=True)
MSD.run()

The MSD can then be accessed as

msd =  MSD.results.timeseries

Visual inspection of the MSD is important, so let’s take a look at it with a

simple plot.

import matplotlib.pyplot as plt
nframes = MSD.n_frames
timestep = 1 # this needs to be the actual time between frames
lagtimes = np.arange(nframes)*timestep # make the lag-time axis
fig = plt.figure()
ax = plt.axes()
# plot the actual MSD
ax.plot(lagtimes, msd, lc="black", ls="-", label=r'3D random walk')
exact = lagtimes*6
# plot the exact result
ax.plot(lagtimes, exact, lc="black", ls="--", label=r'$y=2 D\tau$')
plt.show()

This gives us the plot of the MSD with respect to lag-time (\(\tau\)). We can see that the MSD is approximately linear with respect to \(\tau\). This is a numerical example of a known theoretical result that the MSD of a random walk is linear with respect to lag-time, with a slope of \(2d\). In this expression \(d\) is the dimensionality of the MSD. For our 3D MSD, this is 3. For comparison we have plotted the line \(y=6\tau\) to which an ensemble of 3D random walks should converge.

Note that a segment of the MSD is required to be linear to accurately determine self-diffusivity. This linear segment represents the so called “middle” of the MSD plot, where ballistic trajectories at short time-lags are excluded along with poorly averaged data at long time-lags. We can select the “middle” of the MSD by indexing the MSD and the time-lags. Appropriately linear segments of the MSD can be confirmed with a log-log plot as is often reccomended [Maginn2018] where the “middle” segment can be identified as having a slope of 1.

plt.loglog(lagtimes, msd)
plt.show()

Now that we have identified what segment of our MSD to analyse, let’s compute a self-diffusivity.

4.7.2.2.2. Computing Self-Diffusivity

Self-diffusivity is closely related to the MSD.

\[D_d = \frac{1}{2d} \lim_{t \to \infty} \frac{d}{dt} MSD(r_{d})\]

From the MSD, self-diffusivities \(D\) with the desired dimensionality \(d\) can be computed by fitting the MSD with respect to the lag-time to a linear model. An example of this is shown below, using the MSD computed in the example above. The segment between \(\tau = 20\) and \(\tau = 60\) is used to demonstrate selection of a MSD segment.

from scipy.stats import linregress
start_time = 20
start_index = int(start_time/timestep)
end_time = 60
linear_model = linregress(lagtimes[start_index:end_index],
                                              msd[start_index:end_index])
slope = linear_model.slope
error = linear_model.rvalue
# dim_fac is 3 as we computed a 3D msd with 'xyz'
D = slope * 1/(2*MSD.dim_fac)

We have now computed a self-diffusivity!

4.7.2.2.3. Combining Multiple Replicates

It is common practice to combine replicates when calculating MSDs. An example of this is shown below using MSD1 and MSD2.

u1 = mda.Universe(RANDOM_WALK_TOPO, RANDOM_WALK)
MSD1 = msd.EinsteinMSD(u1, select='all', msd_type='xyz', fft=True)
MSD1.run()

u2 = mda.Universe(RANDOM_WALK_TOPO, RANDOM_WALK)
MSD2 = msd.EinsteinMSD(u2, select='all', msd_type='xyz', fft=True)
MSD2.run()

combined_msds = np.concatenate((MSD1.results.msds_by_particle,
                                MSD2.results.msds_by_particle), axis=1)
average_msd = np.mean(combined_msds, axis=1)

The same cannot be achieved by concatenating the replicas in a single run as the jump between the last frame of the first trajectory and frame 0 of the next trajectory will lead to an artificial inflation of the MSD and hence any subsequent diffusion coefficient calculated.

Notes

There are several factors that must be taken into account when setting up and processing trajectories for computation of self-diffusivities. These include specific instructions around simulation settings, using unwrapped trajectories and maintaining a relatively small elapsed time between saved frames. Additionally, corrections for finite size effects are sometimes employed along with various means of estimating errors [Yeh2004, von Bülow2020] The reader is directed to the following review, which describes many of the common pitfalls [Maginn2018]. There are other ways to compute self-diffusivity, such as from a Green-Kubo integral. At this point in time, these methods are beyond the scope of this module.

Note also that computation of MSDs is highly memory intensive. If this is proving a problem, judicious use of the start, stop, step keywords to control which frames are incorporated may be required.

References

[Maginn2018] (1,2,3)

Edward J. Maginn, Richard A. Messerly, Daniel J. Carlson, Daniel R. Roe, and J. Richard Elliot. Best practices for computing transport properties self-diffusivity and viscosity from equilibrium molecular dynamics. Living Journal of Computational Molecular Science, 1(1):6324, Dec. 2018. URL: https://livecomsjournal.org/index.php/livecoms/article/view/v1i1e6324, doi:10.33011/livecoms.1.1.6324.

[Yeh2004]

In-Chul Yeh and Gerhard Hummer. System-size dependence of diffusion coefficients and viscosities from molecular dynamics simulations with periodic boundary conditions. The Journal of Physical Chemistry B, 108(40):15873–15879, 2004. doi:10.1021/jp0477147.

[von Bülow2020]

Sören von Bülow, Jakob Tómas Bullerjahn, and Gerhard Hummer. Systematic errors in diffusion coefficients from long-time molecular dynamics simulations at constant pressure. The Journal of Chemical Physics, 153(2):021101, 2020. doi:10.1063/5.0008316.